无法建模
Can’t Model It
- 03
- 10
- 2022
在建模软件 Rhino 中选中一个 NURBS 曲面,然后在指令栏里输入“ExtractAnalysisMesh”,我们会得到一个与 NURBS 几何形状几乎相同的网格面(Mesh)。然而这一指令并不常用,也未见得好用。如果要将曲面转变为网格面,只需要输入“mesh”四个字母即可。这不禁让人反思 Rhino 软件的设计师为何“多此一举”。
“数”与“形”
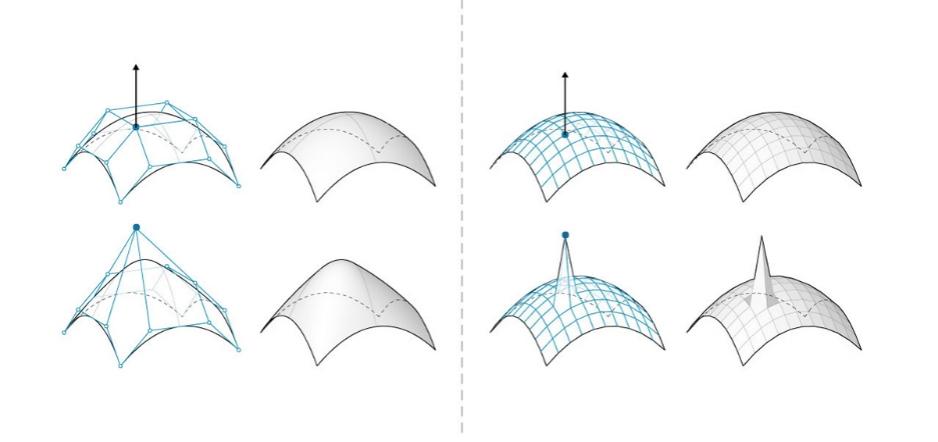
来源:https://primer.dynamobim.org/05_Geometry-for-Computational-Design/5-7_meshes.html.
NURBS 曲面与网格面是记录模型几何信息的两种方式,互有所长。一个 NURBS 曲面的形态基本由若干控制点的坐标所决定,若要具体找到曲面上每个插值点的位置,则需要用公式来计算。要定义一个曲面,真正被 “记录” 的信息仅为少量控制点,而曲面本体是要被实时 “计算” 出样貌的参数方程。与之相反,网格面中的记录远多于计算。它的形状由密密麻麻的顶点坐标所规定,当顶点以最简单的数学形式相连,我们得到直线或平面。我们可以把 NURBS 与 Mesh 类比于矢量图与像素图,前者可以书写成无限精确的数学公式,而后者则是反复放大之后无法阅读的方形色块。
如果要教条地以“真伪”之辩来给二者判个优劣,那么 NURBS 无疑更接近“本质”,而 Mesh 或许更忠于对表象的描述。虽然将世界二分成本质和表象这一假设夹杂有先入为主的褒贬判断,但类似的二元对立在艺术与建筑的历史上的确曾激发出了经久不衰的辨析和创作。无论是结构 – 填充、句法 – 语义、还是抽象 – 具象,这些二元视角均暗示:对世界的探索应当触及其中简洁且恒定的规律,而新世界的创造应来自于某种抽象理念的投射。这种抽象过程的一个极端是数学化,而“形”只是依附在“数”之上的皮肉。这一信条给予了参数化设计正当性:此类设计图板上常见密密麻麻沿格网排列的比较方案。这些千姿百态的建筑形体本身并非赏析的对象──懂行的读者应当知道要越过表象去赞美其背后数学逻辑的简洁与灵活。NURBS 曲面优越于网格面,也是基于类似的观念:几何形体的婀娜不及数学形式的优雅。
本文无意将“数”的优越性阐释成某种宗教信仰,尽管将数学规律视作神的理性在人和建筑上的投射古已有之。“数”优于“形”在建筑这门实践中其实并不失为合理的价值判断。在建筑这项复杂且资源消耗巨大的活动中,建筑师往往无暇兼顾所有细节,只能转而设计某种抽象而关键的系统框架。同时“数”的精确性也建立了不同工种间互信的基础,让建筑实践摆脱巴别塔的困境。这些实在的好处随后才被内化为建筑学的价值取向,因而建筑师群体难免会抱有这样的观点:图纸(drawing)优于图像(image);数优于形;NURBS 优于网格面。
然而,NURBS 曲面的抽象数学公式是如何被绘制在屏幕上被人“看”到的呢?为了能“看”到它的几何形状,电脑要计算每个屏幕像素所对应的曲面上的点位于何处、朝向哪里、深浅如何。在 Rhino 中按住右键随便转转视角就意味着等量于屏幕像素数量的方程要被重新求解。而求解 NURBS 这样看似形式简单的方程并非易事──光是找出曲面和视线相交点的位置就已经困难重重。NURBS 曲面背后数学公式的简洁性此时形同虚设,反而变成徒增计算量的障碍。
事实上,Rhino 并不会直接渲染出 NURBS 曲面,而是时刻用一个与它形状近似的网格面来代替它出现在屏幕之上。这也是开头所述指令的真正作用:将那个替身 Mesh 实例化为场景中的一个物体。换言之,一个 NURBS 曲面无法被直接“看”到,因为它从未被直接渲染。可视的只是它的表征(representation),即网格面的替身。而它的实体则隐藏在计算机深处的数学结构中。
隐匿的数学公式、代为渲染的网格面、渲染出的像素,这三者何为本体,何为表征?我们倘若深究这一问题,恐怕又要落入自说自话的文字游戏中。本文列举这一趣闻只是想论证:数字模型往往不会将所有几何信息一五一十记录下来,而是往往被书写成一段隐形公式,若想要将其在视觉上呈现则要依靠渲染计算。这有别于在现实世界中物体先验地存在,而后才在与光影和人的感官的互动中被再现。某种意义上讲,数字模型不被渲染也就不算完整地存在。
看得见,摸不着
如果说 NURBS 的代码距离尽善尽美地描述几何信息仅仅一步之遥的话,那么下文的情形或许会在根本上动摇人们对于一个完备数字模型的信念。
分形(fractal)物体即是一个无法用数字模型记录,却可以用图像实时表现的形体。伴随着《湮灭》《奇异博士》等院线影片在视觉特效上对分形的应用,这些一边流动一边变异的几何体、重重嵌套无止尽的空间逐渐成为数字视觉艺术的新宠。与 DeepDream、戴维・琼斯(Davy Jones)等这个时代迎来的视觉刺激一道,它既迎合又塑造了我们对于当下混沌、怪异世界的想象,是清醒者的致幻剂。

分形,简而言之即是图形拥有无限的细节,随着视点不断贴近,新的细节徐徐展开。在解释分形概念时,一个常用例子是地图上岛屿的海岸线:在世界地图中绘制一个岛屿,想必岛屿的岸线所能显示的细节有限。而到了国家地图乃至比例尺更大的区域地图,岸线的细节也会逐渐呈现。除了在自然界中寻觅,分形图案也可以通过数学方法建构。其方式五花八门,但大多运用迭代的手段,即定义一种往复的操作,而当这一操作被重复无限多次时即可生成分形。妄图精确找到分形上每个点的位置显然是徒劳,不仅因为无限的几何细节意味着无限复杂的计算,更因为分形无法被抽象成点线面这些基本单元的组合。因此,无论是 NURBS,网格面,或是体素等其他建模方法,都注定无法精确地描述它的几何形态。
然而,这些无法被建模的形体却可以被准确渲染成图像,或者只能以图像的形式被“准确”呈现。准确二字要加上引号是因为所谓准确与否的前提是显示屏只有有限个像素点。随着视角的移动,屏幕所包含的内容以及该分辨率下所能捕捉到的精细程度也会变化,但实时更新的渲染程序会保证当前视角下的分形依然被准确无误地表现。因而,分形的渲染包含这样一种微妙的辩证关系:它确切的空间形态并未被计算机记录,但透过屏幕我们却可以从任意角度观看它的样貌。而且在有限的分辨率下,屏幕精确地展现了它的无限细节。
分形渲染的怪异之处不止于此。首先,分形并非新鲜的发明。《湮灭》中用来描绘外星生物形象的曼德博球分形渲染的怪异之处不止于此。首先,分形并非新鲜的发明。《湮灭》中用来描绘外星生物形象的曼德博球(Mandelbulb)于 1997 年被构建出来,而分形的数学研究从 20 世纪初就已开始。它在屏幕上的普及,除了得益于图形硬件的进步,还依赖新颖的渲染方法。传统渲染方法如光线追踪(ray tracing)在渲染分形上力不从心,与其本身的原理相关。光线追踪算法从视点穿过每个像素向场景中逆向发射搜索射线,这些射线与场景中的几何体相交后,渲染器进而找到交点,并根据交点处的几何和材质信息来计算该交点的明暗,也就是对应像素的色彩。然而对于分形这样拥有无限细节的物体,单靠寻找交点自然是无法完成任务的。如今屏幕上异彩纷呈的分形图像很多依靠另一算法:光线行进(ray marching)。相比于光线追踪,光线行进更像是盲人摸象:同样是从视点发射出搜索射线,但射线并不直接穿过场景以求得交点,而是步步为营,逐渐逼近几何体而并不与之相交。搜索射线最终会停在与几何体表面十分接近的位置。当然,停留位置越接近分形表面,渲染图像越高清,所需计算也越多。巧妙的是,曼德博球的数学定义恰好方便了光线行进算法估算射线在每一步与分形的距离,这等同于在黑暗中摸索的渲染器得以估计出分形的位置,那么它的明暗、颜色等属性也就迎刃而解,我们从而能一睹曼德博球的真容。①
光线行进进一步启发我们去质疑建模和渲染、本体与表征间的边界是否存在。诸如曼德博球这样的几何体,其记录在计算机中的只是简单的迭代方程,而真正寻找它的几何边界──换言之,“建模”的行为──则发生在渲染器的摸索过程里。
以上辨析或许在计算机领域无关痛痒,却有助于更新我们对建筑的某些固有认知,如模型和图像的二分,以及几何之于图像的优先顺序。正如效果图和技术图纸之间的分工:我们依赖图像来理解几何信息,却将那个记录建筑各点坐标的模型视作行业间互信的基准──无论它如何抽象且不完善。图像被用来勾勒彼此的意图,但模型和图纸才是不动的铁证。绕开模型并由图像直接描述建筑甚至指导建筑落成通常难以成立,不仅因为这在文化上违背了建筑正统,更因为技术上而言,从图像到建筑的转译含混不清,而且图像本身也模糊且片面。这使得建筑传统中图像对建筑的指涉注定是启发式的。其困境正如布瓦(Yve-Alain Bois)对皮拉内西画作中建筑空间的重构一样──将图像笨拙地重构成确切的三维空间后,实际的空间却和设想大相径庭。②
然而,图像到建筑的转译正变得有迹可循。近年来若干技术在建筑设计中的应用提供了从图像到三维空间的新颖路线,如摄影测量术(photogrammetry)可以通过一个物体各个方向的图像计算出物体的几何信息,而人工智能技术的某些应用也让我们能愈发便捷地将一张二维图像还原成三维空间。③ 逐渐发展的计算力允许我们挖掘出寄宿于图像中的空间信息。有朝一日,当从图像到空间的转译不仅快捷而且逻辑清晰,届时图像是否也能成为可靠的设计工具?依靠图像而想象出的新世界又会和建模描述的世界有何不同?
而模糊又片面的图像也终将变为全息。它所能蕴含的信息或许无法比肩现实的复杂度,但不难达到人类感知的上限。在 2009 年发表的“为低清图像辩护(In Defense of the Poor Image)”一文中,艺术家黑特・史徳耶尔(Hito Steyerl)将低清图像视作高效、平等的知识传播载体。这得益于低清图像在突破版权壁垒时的“灵活身法”,也因为图像的压缩并不影响观点的传达。④ 然而,随着 4K、IMAX 等制式遍及日常生活,高清图像塑造了当下的审美体验。我们习惯于凝视图像,沉浸于图像本身。高清图像也不仅是观点的载体。它所激发的感官互动并不能用言语或几何概括。图像不可被精确地言说,也无法被完善地建模,但它却比语言和模型都更能触及世界的复杂与真实。
- 如今分形渲染的普及得益于 2010 年左右起于网络社区兴起的自发分享,并依靠 Shadertoy 等线上平台的进一步推广。学者、艺术家多利用博客分享个人项目和代码,其中影响广泛的人物包括 Iñigo Quilez、Mikael Hvidtfeldt Christensen 等。后者的博客就详细介绍了曼德博球渲染背后的数学规律,阐明了为何光线行进可以巧妙地计算出分形的图像。博客地址:http://blog.hvidtfeldts.net/
- 参见:Hito Steyerl, “In Defense of the Poor Image,” e-flux Journal 10, no. 11 (2009).
- 神经辐射场(Neural Radiance Field)技术可以通过利用少量图片推测生成完整的三维环境。
- 参见:Yve-Alain Bois, and John Shepley, “A Picturesque Stroll around ‘Clara-Clara’,” October 29 (1984): 33-62.







http://www.matlab.com
1xBet является одной из самых известных на рынке. https://bet-promokod.ru/ Огромный выбор событий из мира спорта и киберспорта, множество открытых линий, самые высокие коэффициенты. Также, БК имеет обширный функционал и одна из немногих дает возможность совершать ставки по специальным промокодам. Используя их, вы можете получить настоящие деньги, не внося абсолютно никаких средств. Это реально! Узнать последний промокод вы можете сейчас же, однако использовать его необходимо в соответствии с правилами и инструкциями, которые приведены ниже.
https://freight.cargo.site/w/1250/i/82e05d61b9f549c45160e1adaab1d14aa7b6c3f86eb4d7077b50d9c87a769187/0208_Poster_PlasticUp_FINAL-JS-01_small---background.gif
https://freight.cargo.site/w/1250/i/fbfc32bc70ac9d619d1557654d60e4e3d4bc629d8f1f89473a57c6abb68fa3d8/Banners_large.gif
https://www.rhino3d.com/features/nurbs/
http://docs.mcneel.com/rhino/5/help/en-us/commands/mesh.htm
http://docs.mcneel.com/rhino/5/help/en-us/commands/extractanalysismesh.htm
https://en.wikipedia.org/wiki/Polygon_mesh
https://www.rhino3d.com/
https://en.wikipedia.org/wiki/The_Unreasonable_Effectiveness_of_Mathematics_in_the_Natural_Sciences
https://images.squarespace-cdn.com/content/v1/5ced36ad9fb4bd00016b8138/1560179965957-KT0DUCBFWTJQKWDVUNB1/Piero de la Francesca, foreshortened head, de_prospectiva_pingendi,_ante_1482,_milano,_biblioteca_ambrosiana Wikimedia.jpg?format=2500w
https://www.pacegallery.com/media/images/897915keypj_7RZsaJCBzsAwpRo4rDQ.width-2000.jpg
https://www.artnews.com/wp-content/uploads/2019/07/hs14-0019-presspage-e1563470016999.jpg
https://www.youtube.com/watch?v=NJCiUVGiNyA
https://pic3.zhimg.com/80/v2-6410db0e15ae363d88985a47a7be67ae_1440w.jpg
https://zhuanlan.zhihu.com/p/111921190
https://primer.dynamobim.org/05_Geometry-for-Computational-Design/5-7_meshes.html
https://imagen.research.google/
https://thepracticeofdrawing.org/proportion-perspective-page
https://images.squarespace-cdn.com/content/v1/5ced36ad9fb4bd00016b8138/1560179940737-2RE567XLP86ERK3GE7B6/Paolo_uccello,_studio_di_vaso_in_prospettiva_02.jpg?format=2500w